Neural network architecture and activation functions

Welcome to this lesson on neural network architecture and activation functions in bioinformatics! We have designed this lesson for university students interested in learning about the basics of neural networks and how to apply them applied in bioinformatics.

Before diving into the details, let's start by understanding what neural networks are and how they work.

The Basic Structure of Neural Networks

Neural networks consist of many interconnected "neurons," which process and transmit information. The input data is processed through the network, layer by layer until it reaches the output layer, where a network model makes a prediction or decision.

The structure of a neural network is composed of an input layer, hidden layers, and an output layer. The input layer receives and passes the data to the hidden layers. The hidden layers process the data and give it to the output layer, where a network model makes a prediction or decision for output.

We can vary the number of hidden layers and neurons in each layer. The number of layers and neurons required depends on the complicatedness of the problem at hand.

Activation Functions

Now that we have a basic understanding of neural networks, let's discuss activation functions. Activation functions are mathematical functions that determine the output of a neuron given an input or set of inputs. They introduce non-linearity to the network, allowing it to learn and model more complex relationships in the data.

It is possible to use several different activation functions in a neural network, including sigmoid, tanh, ReLU (Rectified Linear Unit), and leaky ReLU.

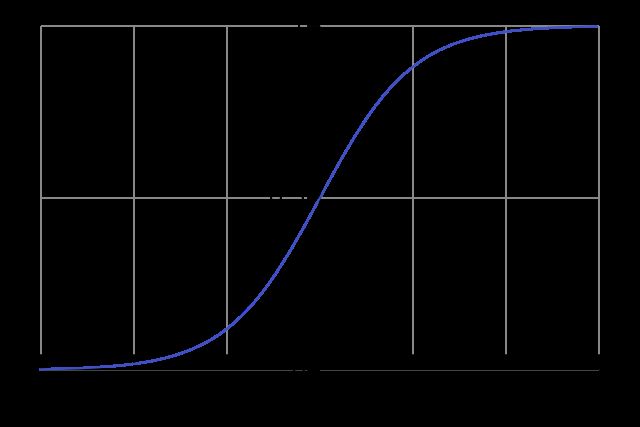
Sigmoid function

The sigmoid function is a smooth, S-shaped curve that maps any input value to a value between 0 and 1. It is often used in the output layer of a binary classification problem, where the output represents the probability of a specific class. However, the sigmoid function can suffer from vanishing gradients, making it difficult for the network to learn and improve.

Tanh function

The tanh function differs from the sigmoid function by mapping input values to a range of -1 to 1. It is also smooth and S-shaped but has a broader range of output values than the sigmoid function.

ReLU (Rectified Linear Unit) function

The ReLU (Rectified Linear Unit) function is a linear function that returns the input value if it is positive and 0 if it is negative. It is fast to compute and has been shown to work well in many deep-learning applications. However, it can suffer from the problem of "dying neurons" problem where the output is always 0, which can prevent the network from learning.

Leaky ReLU function

The leaky ReLU function differs from the ReLU function by allowing a slight negative slope for negative input values. The small negative values help to prevent dying neurons and enable the network to continue learning.

In bioinformatics, neural networks have been applied to a wide range of problems, including protein folding prediction, gene expression analysis, disease diagnosis, and predicting protein structures using their amino acid sequence. The predictions are useful in drug design, as the structure of a protein can determine its function and potential interactions with other molecules.

Proceed to the next lecture: Training neural networks using backpropagation

References